На двух не параллельных прямых взяты равные отрезки:
АА₁ = А₁А₂ = … = А₆А₇ на одной, ВВ₁ = В₁В₂ = … = В₆В₇ на другой.
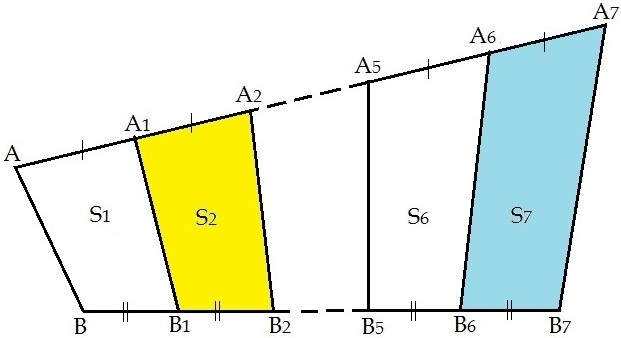
Проведены отрезки АВ, А₁В₁, …, А₇В₇. См. рисунок.
Площади двух, из семи получившихся, четырехугольников известны: S₂ = 3, S₇ = 13.
Какова площадь четырехугольника АВВ₇А₇ ?
подробнее о бонусах
бонус за лучший ответ: 7 кредитов
хотите увеличить?
тэги:
геометрия,
математика,
площадь
категория:
образование
ответить
комментировать
в избранное
бонус
2 ответа:
старые выше
новые выше
по рейтингу
4

габбас
[95.7K]
4 дня назад
Площади фигур АА1В1В, А1В2В1, и т.д. образуют арифметическую прогрессию, где второй член равен 3, а седьмой — 13. Поэтому воспользуемся формулой суммы арифметической прогрессии. Для этого найдем разность арифметической прогрессии d и ее первый член a1. Так как a2 = 3, a7 = 13, то по формуле энного члена арифметической прогрессии а2 = а1 + d, а7 = а1 +6*d , исключаем а1 и получим 5*d = 13-3 или d=2. Тогда а1 = а2-d = 3-1 =1. S = (a1+a7)/2 *7 = (1+13)*7/2, получим что площадь данного четырехугольника АВВ7А7 равен 49.
в избранное
ссылка
отблагодарить
FEBUS
[469]
Наверное А1А2В2В1.
Откуда следует, что … "образуют арифметическую прогрессию" ?
— 3 дня назад
габбас
[95.7K]
Если провести из Вершины А прямую параллельную ВВ7, то полученные треугольники образуют арифметическую прогрессию, значит и четырехугольники тож.
— 3 дня назад
FEBUS
[469]
Это почему? Это неверно, очевидно.
— 3 дня назад
комментировать
1
Rafail
[104K]
3 дня назад
Продолжим прямые АА7 и ВВ7 до их пересечения в точке О. Обозначим угол АОВ фи, длину ОА х, длину ОВ у. Площадь треугольника АОВ обозначим S0. Обозначим длины отрезков АА1=А1А2=…а, ВВ1=В1В2=… в.
Найдём площади получившихся треугольников по формуле через синус угла:
S(АОВ)=0,5*sin(фи)*х*у=S0;
S(А1ОВ1)=0,5*sin(фи)*(х+а)*(у+в)=0,5*sin(фи)*x*y*+0,5*sin(фи)*SHY=S0;
S(А2ОВ2)=0,5*sin(фи)*(х+2а)*(у+2в)=0,5*sin(фи)*x*y*+0,5*sin(фи)*(2вx*2ау*+4ав);;
………………..…….
S(А7ОВ7)=0,5*sin(фи)*(х+7а)*(у+7в).
*********************
Обозначим для краткости множитель 0,5*sin(фи) буквой К.
S7=S(А7ОВ7)-S(А6ОВ6)=К*(х+7а)*(у+7в)-К*(х+6а)*(у+6в)=К*(вх+ау+13ав);
S2=S(А2ОВ2)-S(А1ОВ1)=K*((х+2а)*(у+2в))-K*SHY=K*(вх+ау+3ав);
Отношение S7/S2=13/3. Подставляя выражения для S7и S2 получаем:
(вх+ау+13ав)/(вх+ау+3ав)=13/3. Приводя к общему знаменателю получаем: 3вх+3ау+39ав=13вх+13ау+39ав, т.е. 10*(вх+ау)=0. Поскольку и а и в — по определению положительные числа, это условие выполнимо только при х=0, у=0.
Отсюда следует, что точки О, А и В совпадают.
Теперь видно, что S(i)=(i^2-(i-1)^2)*ав=(2*i-1)*ав и величины S1///S7 образуют арифметическую прогрессию: 1, 3, 5, 7, 9, 11, 13, так что габбас прав.
Пллощадь четырёхугольника АА7В7В (точнее, треугольника ОА7В7) равна 49.
в избранное
ссылка
отблагодарить
FEBUS
[469]
Конечно, вообще говоря, неверно, что "Отсюда следует, что точки О, А и В совпадают."
Числа так неудачно подобраны.
— 3 дня назад
Rafail
[104K]
х — это расстояние ОА, у — расстояние ОВ. Если вычисления привели к значениям, х=0 и у=0, из этого следует, что точки О и А (или О и В) совпадают.
— 3 дня назад
FEBUS
[469]
Да, это в данном частном случае.
В общем случае, в приведенных обозначениях
S1 = (1 + a/x)(1 + b/y)So — So = (a/x + b/y + ab/xy)So
S2 = (a/x + b/y + 3ab/xy)So
S3 = (a/x + b/y + 5ab/xy)So.
Откуда все следует.
Что еще за SHY ?
— 3 дня назад
Rafail
[104K]
Но соотношение S7:S2=13:3 возможно только в такой ситуации, когда точки А и В совпадают.
— 3 дня назад
Rafail
[104K]
SHY — это "чудеса самостоятельности" текстового редактора БВ. Мне довольно часто приходится бороться с его выкрутасами. Разумеется, там, где появилось "SHY" я писал нормальное выражение (х+а)*(у+в). А почему при доставке оно превратилось в "SHY", я не знаю.
— 3 дня назад
комментировать
