Чему равен шаг эвольвенты окружности?
тэги:
задача,
математика,
наука,
решение
категория:
наука и техника
ответить
комментировать
в избранное
бонус
4 ответа:
старые выше
новые выше
по рейтингу
2
![]()
Грустный Роджер
[193K]
1 неделю назад
Штука в том, что шаг эвольвенты (если под её шагом считать расстояние между точками пересечения эвольвенты с какой-нибудь из осей) переменный. Это легко понять даже из ответа spin’a, хоть он и не совсем верен.
Да, с каждым новым витком будет добавляться ещё одна длина окружности. Но тонкость тут в том, что этот новый шаг отсчитывается по касательной к исходной окружности, а не по нормали. Да, по мере удаления от окружности (с увеличением "номера витка") этот шаг будет всё ближе и ближе к 2пи, но никогда не станет равным ему точно.
Ну и попробуем дать строгую оценку шага.
Параметрические уравнения эвольвенты для окружности единичного радиуса выглядят так:
x(t) = cos(t) + t*sin(t)
y(t) = sin(t) — t*cos(t)
Возьмём для примера точки пересечения эвольвенты с положительной частью оси Х, чему соответствует у=0. Мы приходим к трансцендентному уравнению sin(t) — t*cos(t) = 0. Аналитически такое уравнение не решается, однако численное его решение получить не штука хотя б в Экселе или на Вольфраме. Как нетрудно убедиться, эти точки будут располагаться на следующих координатах (значения округлённые): 1; 7,79; 14,1; 20,4; 26,68…
Тем самым шаг эвольвенты вдоль положительного направления оси Х будет таким: 6,79; 6,31; 6,294; 6,289…
Как видите, он всё ближе и ближе к 2пи (6.283185307…), но — непостоянен.
Аналогично можно определить и шаг вдоль любой другой полуоси.
в избранное
ссылка
отблагодарить
bezdelnik
[26.8K]
Интересное дополнение, но не имеющее практического применения. Практически эвольвента используется на небольшом участке не превышающем 0,05 длины начальной окружности, и не может иметь даже одного шага
— 1 неделю назад
spin
[14.6K]
Дополнение интересное, но, к сожалению, не верное.
Действительно, шаг эвольвенты отсчитывается по касательной к окружности. Ведь именно на окружности намотана мнимая нить.
То, что Вы посчитали — совсем другой отрезок. Параметрическое уравнение, которое указано в ответе, правильное. Но! Единичная окружность имеет центр в начале координат. Поэтому ось Ох не есть касательной к окружности!
— 1 неделю назад
spin
[14.6K]
Если не верите — нарисуйте рисунок (к сожалению, в комментариях вложить рисунок не могу).
— 1 неделю назад
Грустный Роджер
[193K]
bezdelnik, тут речь не о практическом применении, а о чисто теоретической задачке: свойствах кривой, заданной неким параметрическим уравнением. То, что эта кривая имеет ещё и некоторое практическое применение, — факт интересный, но отношения к вопросу не имеющий.
— 1 неделю назад
Грустный Роджер
[193K]
spin, в таком случае всё упирается в то, как считать шагом эвольвенты. Если шаг определяется как точки пересечения с осями, или с произвольной прямой, проходящей через центр окружности, — то мой ответ верен. Если шаг определять по прямой, касательной к окружности, то верен ваш ответ.
— 1 неделю назад
spin
[14.6K]
Я всегда был уверен в том, что шаг считается по перпендикуляру (нормали) к самой линии. Также, как расстояние между параллельными прямыми, плоскостями и т.п.
— 1 неделю назад
все комментарии (еще 1)
комментировать
2
![]()
Mefody66
[27.7K]
1 неделю назад
Я вижу, вы начитались господина Александра Белкина про плоскую Землю и силу Кориолиса?
Он сетует, что силу Кориолиса, чисто физическое понятие, не ввели в математику.
Сила Кориолиса — это сила, которая сдвигает русла рек в направлении вращения Земли.
А эвольвента окружности здесь вообще ни при чем.
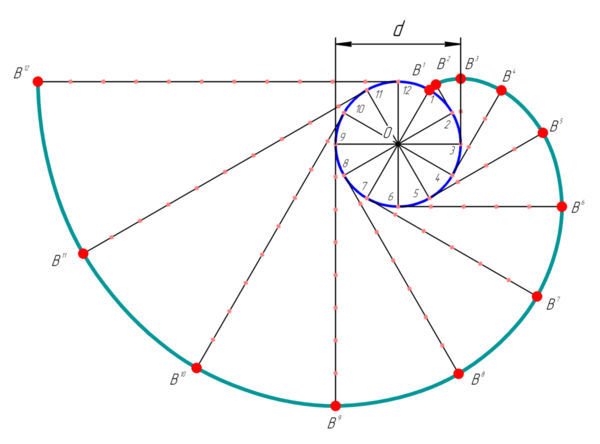
Это спираль, которая является разверткой окружности на плоскости, и определяется так:
Это такая кривая, что любая касательная к окружности перпендикулярна касательной к эльвольвенте в точке их пересечения.
Вот на рисунке все понятно.
Эвольветна окружности — это спираль с постоянным шагом, то есть расстояние между витками не изменяется.
Шаг эвольвенты равен длине окружности.
комментировать
в избранное
ссылка
отблагодарить
2
bezdelnik
[26.8K]
1 неделю назад
Эвольвента это кривая получающаяся при качении линейки по окружности, которую в данном случае называют начальной окружностью. Конец линейки приложенный к начальной окружности очерчивает эвольвенту при качении линейки по начальной окружности без скольжения. У эвольвенты не может быть ни какого шага. Возможно автор спрашивает о шаге между зубьями у зубчатых колес с эвольвентным зацеплением. Для определения такого шага надо знать модуль зацепления m который равен длине начальной окружности d деленной на количество зубьев Z колеса: m = d/z. Модули стандартизированы по ГОСТ 9563 – 60.
в избранное
ссылка
отблагодарить
lostparadise
[25.2K]
Просто недавно прочитал статью https://www.telegraf.in.ua/kremenchug/10069282-k-voprosu-o-tom-chto-zemlya-ploskaya-kremenchugskiy-matematik-obeschaet-tysyachu-dollarov-za-otvet-na-ego-vopros.html
и стало интересно мнение по этому поводу.
— 1 неделю назад
комментировать
2
spin
[14.6K]
1 неделю назад
Шаг эвольвенты окружности равен длине этой окружности.
Чтобы нарисовать эвольвенту, надо на окружность навинуть нерастяжимую нить. К концу нити привязать карандаш. При разматывании нити в одном направлении карандаш будет рисовать линию. Это и будет эвольвента. Она подобна плоской спирали.
Ясно, что при если сделать один оборот, то карандаш будет от окружности на расстоянии длины окружности. Если еще раз развинуть нить, то расстояние от окружности до карандаша будет равно двум длинам окружности. И так далее. Т.е. между витками всегда будет длина окружности. Это и будет шаг.
в избранное
ссылка
отблагодарить
Грустный Роджер
[193K]
Хотя шаг эвольвенты действительно (почти) равен длине окружности, утверждение "если сделать один оборот, то карандаш будет от окружности на расстоянии длины окружности" — неверное. На расстоянии длины окружности он будет не от самой окружности, а от точка касания, если касательную провести вот от той точки эвольвенты, которая и соответствует ровно 1 полному обороту.
— 1 неделю назад
spin
[14.6K]
Шаг эвольвенты меряется по нормали к самой эвольвенте. Эта нормаль будет касательной к окружности. Это следует из определения эвольвенты.
Поэтому шаг не "почти", а точно равен длине окружности. Если мнимую нить развинуть на один виток, то получится точно длина окружности. И так будет повторяться с каждым новым витком. Окружность то не меняется. Поэтому длина ее постоянна.
— 1 неделю назад
spin
[14.6K]
В ответе я не написал, что это будет касательная. Думал, что это само собой разумеется. Нить ведь намотана на окружность.
— 1 неделю назад
комментировать
