которой лежит ромб с диагоналями, равными 10 и 24, и боковым ребром, равным 17
тэги:
площадь боковой поверхности,
прямая призма
категория:
образование
ответить
комментировать
в избранное
бонус
1 ответ:
старые выше
новые выше
по рейтингу
1
vdtest
[20.3K]
3 дня назад
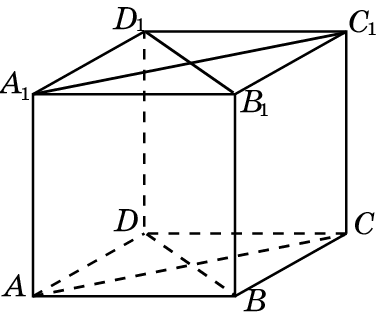
В ромбе диагонали пересекаются под прямым углом и в точке пересечения делятся пополам.
Ромб в основании призмы разделяется диагоналями на четыре прямоугольных треугольника у которых один катет равен 10/2=5, а другой равен 24/2=12
По теореме Пифагора гипотенуза каждого треугольника равна
AB=BC=CD=AD=√(5² + 12²) = √(25 + 144) = √(169) = 13
Площадь боковой поверхности призмы равна сумме площадей четырёх прямоугольников ABB₁A₁, BCC₁B₁, CDD₁C₁, DAA₁D₁ и равна
Sбок = 4 × 13 × 17 = 4×221 = 884
Ответ
Площадь боковой поверхности прямой призмы, в основании которой лежит ромб с диагоналями 10 и 24 и высотой 17 равна 884.
комментировать
в избранное
ссылка
отблагодарить
