Дано:
X-Y=Z (1);
Произведя арифметические действия, доказать или опровергнуть возможность представления уравнения (1) в матричном виде.
тэги:
математика,
матричное произведение,
мкэ
категория:
наука и техника
ответить
комментировать
в избранное
бонус
2 ответа:
старые выше
новые выше
по рейтингу
0
VictorNeVrach
[5.2K]
2 недели назад
Для того что бы доказать или опровергнуть возможность записи уравнения (1), как произведение матриц, необходимо вспомнить простое свойство и произвести проверку.
См. рисунок.
Из рисунка становится очевидно, что Z — любое вещественное число, а значит само Z существует как разность вещественных чисел так и как перемножение матриц, а конкретно вектора строки на вектор столбец.
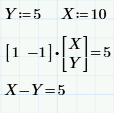
комментировать
в избранное
ссылка
отблагодарить
0
![]()
Грустный Роджер
[309K]
2 недели назад
Скорее всего, нет, потому что тут стоит знак "минус", которым обычно обозначается операция вычитания, а не перемножения. Хоть чисел, хоть матриц.
Но без знания того, что такое X, Y и Z, определённо судить трудно…
в избранное
ссылка
отблагодарить
VictorNeVrach
[5.2K]
X, Y, Z — просто числа, но которые вполне считаются и элементами матриц при определенных условиях.
— 2 недели назад
Грустный Роджер
[309K]
А (1) — это просто номер формулы или что-то осмысленное?
— 2 недели назад
VictorNeVrach
[5.2K]
Ну обычно так пишут номер уравнения или формулы, (1) — это просто ссылка, что бы по тексту сразу ссылаться на формулу.
— 2 недели назад
Грустный Роджер
[309K]
Ну тогда сама формула есть просто вычитание одного объекта из другого. По фигу чисел или матриц. Умножением не пахнет.
— 2 недели назад
VictorNeVrach
[5.2K]
Вы наверное не знакомы с МКЭ) Это именно произведение.
— 2 недели назад
комментировать
