Известен также острый угол при вершине А и разность сторон АВ и ВС, причём АВ больше ВС.
тэги:
геометрия,
задача
категория:
образование
ответить
комментировать
в избранное
бонус
3 ответа:
старые выше
новые выше
по рейтингу
2
Анатолий-тдр5
[12K]
3 дня назад
Мы никак не сможем разность отложить, если это просто число. Поэтому нужно предположить, что эта разность уже задана в виде отрезка, длина которого равна разнусти двух сторон (АВ и BC треугольника ABC), длину которого обозначим d.
Тогда построение можно выполнить в следующей последовательности.
Строим треугольник ADC по известным сторонам AC и d (разность AB-BC) и углу A. Т.е. на стороне угла А откладываем из вершины с помощью циркуля отрезки АС и AD=d, соединяя затем отрезком точки С и D.
Затем строим серединный перпендикуляр стороны СD. Пересечение этого перпендикулярв с лучом AD даст вершину B искомого треугольника. Соединяем отрезками B c точками A и С. Треугольник ABC построен.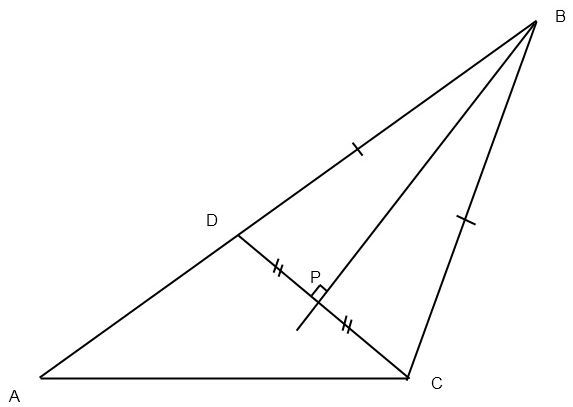 Обоснованием служат следующие рассуждения. Если треугольник ABC уже построен, то отложив из B на стороне AB отрезок BD=BC, получим равнобедренный треугольник BDC, вершина B которого лежит на серединном перпендикуляре. Но AD в таком случае будет разностью сторон AB и BC, причём AB>BC.
Обоснованием служат следующие рассуждения. Если треугольник ABC уже построен, то отложив из B на стороне AB отрезок BD=BC, получим равнобедренный треугольник BDC, вершина B которого лежит на серединном перпендикуляре. Но AD в таком случае будет разностью сторон AB и BC, причём AB>BC.
в избранное
ссылка
отблагодарить
Евгений Борисович
[795]
Анализ не сделан.
Такое построение возможно не всегда.
— 3 дня назад
Анатолий-тдр5
[12K]
Ага. Разность сторон должна быть меньше третьей стороны, что является следствием неравенства треугольника. Врочем, проверить это можно по конкретным исходным данным, о которых ничего неизвестно кроме того, что есть. Поэтому в решение можно внести как раз эту проверку. И ещё должны обосновать, почему в построении угол А — острый (следует из неравенства AB>BC)
— 3 дня назад
Евгений Борисович
[795]
Неверно, что "Разность сторон должна быть меньше третьей стороны".
И в этом случае построение не всегда возможно.
Угол А острый по условию.
— 3 дня назад
Анатолий-тдр5
[12K]
Ну да, острый по условию. Но лихо вы разделываетесь с общеизвестными теоремами. Это "Теорема о неравенстве треугольника для разности двух сторон". Впрочем, даже у Погорелова есть такая задача: "Докажите, что любая сторона треугольника больше разности двух других его сторон". Хотя, может, вы имели в виду что-то другое? Но допустим, что это условие всё же выполняется. Какие могут быть препятствия к построению не по этой, так по другой схеме? Если AB-BC>0, то AB>BC и (<С)>(<А) (против большей стороны лежит больший угол). На чертеже разобран случай тупого <С. Пусть теперь он прямой. Та же схема построения будет работать. Пусть теперь — острый. Так как (<С)>(<А) , то схема будет тоже работать (точка D окажется между А и В. Случай (<С)<=(<А) не имеет смысла рассматривать — это противоречит полученному результату (<С)>(<А)
— 3 дня назад
Анатолий-тдр5
[12K]
Единственным препятствием вижу случай для тупого угла B, когда <А=180°-<B. Но предполагаю, что условие AB-BC>0 не может привести к этому результату, т.к. AB и BC заведомо конечные числа
— 3 дня назад
Евгений Борисович
[795]
Вы неверно понимаете условие задачи на построение. Отсюда и неверное, в принципе, решение.
Надо сказать, что формулировка, конечно, "разговорная" …
Перевожу.
Даны два отрезка n и b, и угол α < 90º.
Построить △ABC, в котором ∠A = α, AC = b, AB − BC = n.
P.S. Это задача с параметрами n, b и α. И вовсе не обязательно, что n < b.
Но, если даже так, то это не означает, что построение возможно.
— 3 дня назад
Анатолий-тдр5
[12K]
Пока только вижу, что при n<b*cos(α) построение по чертежу выше, а при b*cos(α)<=n решения предположительно нет (но способ по чертежу точно не пригоден при любом α)
Что касается случая n>=b при любом α, то решений нет, т.к. опровергнуть следствие неравенств треугольника |n|<b не получается (вообще-то это теорема). К тому же по условию n=AС изначально, а b объявлено, как разность двух других сторон. Т.е. для величин n и b в условии задачи сильная привязочка, а не просто отрезки.
— 3 дня назад
bezdelnik
[30.4K]
Анатолий-тдр5, на вашем рисунке разность сторон АВ-ВС=AD. Для практического построения AD может быть задан числом, например в см, или в виде произвольного отрезка. Второй рисунок мне не понятен.
— 2 дня назад
Анатолий-тдр5
[12K]
Это я и имел в виду, что АВ задан в виде отрезка, т.к. построение предполагается выполнять с помощью циркуля и линейки без делений. А вот числом был бы неудобно, т.к. совершенно точно число на отрезке при построении не отложишь. Второй рисунок — это рассмотрение невозможности выполнить построение в некоторых случаях. Более подробно эти случаи рассмотрены на рисунке там, где гипербола.
— 2 дня назад
все комментарии (еще 4)
комментировать
1
Анатолий-тдр5
[12K]
2 дня назад
Более подробно посмотрим на возможность разрешимости задачи.
Постоянная разность AB-BC=2a (2a<AC=2с) указывает на то, что т.С обязана принадлежать гиперболе с межфокусным расстояием AC=2с.
Разрешимость будет зависеть от выполнения условия 2a<AC и возможности построить точку B на правой ветви гиперболы. Если угол ά меньше угла наклона ассимптоты (1-го и 3-го коорд.углов), то луч из A пересечёт правую ветвь гиперболы, на которой AC>BC. И, следовательно, задача разрешима (конкретный способ построения не рассматриваем). Если угол ά больше или равен углу наклона указанной ассимптоты, то луч пересечёт только левую ветвь, на которой неравенство AC>BC не выполняется.
Таким образом, чтобы построить треугольник по исходным данным, необходимо выполнение условий: 1) AB-BC<AC 2) угол альфа меньше угла наклона правой ассимптоты.
Ассиптота справа имеет уравнение x/a-y/b=0, y=(b/a)*x, где большая полуось гиперболы находится из соотношения b^2=c^2-a^2.
Тангенс наклона ассимптоты к оси Ox равен b/a. Поэтому требуется, чтобы и тангенс угла ά был меньше b/a.
Проверить это можно, предварительно построив прямоугольный треугольник с катетом а и гипотенузой с, т.к. b будет вторым катетом (в виду подобия удобнее конечно брать 2a и 2c, т.к. это длины заданных сторон).
Поэтому задача разрешима только в одном случае, когда одновременно выполняются два условия:
1) длина стороны AC=2c больше длины отрезка AB-BC=2a
2) Заданный угол меньше угла прямоугольного треугольника с катетом "a" и гипотенузой "с", т.е. угла, лежащего напротив построенного катета b.
После этого выполняем построение по схеме, предложенной в первом ответе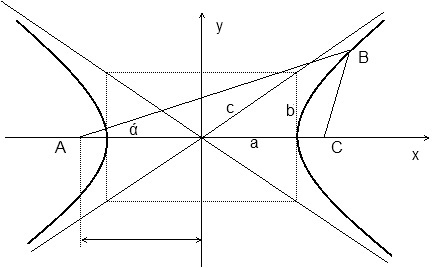
в избранное
ссылка
отблагодарить
Евгений Борисович
[795]
Перемудрено.
— 2 дня назад
Анатолий-тдр5
[12K]
Вы бы предложили свой план, хотя бы схематично (не обязательно чертежи и формулы)
Особенно интересует случай возможности построения треугольника при AC<=|AB-BC|
А то ведь заинтриговали
— 2 дня назад
Евгений Борисович
[795]
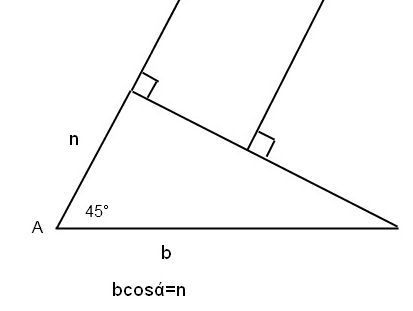
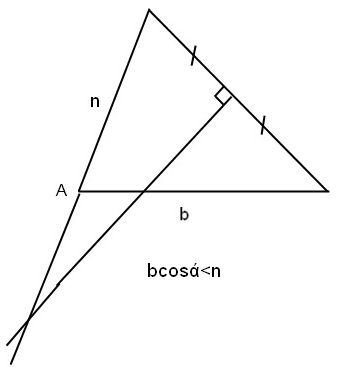
При n ≥ b·cosα такого треугольника нет.
При n < b·cosα есть один.
— 2 дня назад
Анатолий-тдр5
[12K]
Не спорю. Но остаётся только геометрическое построение для проверки этих условий. Т.к. автор задачи уточнил, что величины заданы геометрически. Можно было бы построить круг диаметром b и в нём построить прямоугольный треугольник с углом ά, тогда n должно оказаться меньше прилежащего к углу катета.
— 2 дня назад
комментировать
0
Анатолий-тдр5
[12K]
3 дня назад
//дополнение к ответу для Евгений Борисович[793]
комментировать
в избранное
ссылка
отблагодарить
