Ромб с углами 60° и 120° стоит, опираясь острым углом на плоскость.
Каким должен быть угол alpha между ромбом и плоскостью (показан дугой), чтобы в проекции ромба на плоскость получился квадрат?
Ответ дать в градусах.
подробнее о бонусах
бонус за лучший ответ: 20 кредитов
хотите увеличить?
тэги:
геометрия,
математика,
проекция
категория:
образование
ответить
комментировать
в избранное
бонус
6 ответов:
старые выше
новые выше
по рейтингу
3
![]()
smog2605
[13.2K]
2 дня назад
Наверное не повториться не получится, но тем не менее.
Отличие квадрата от ромба в его равных диагоналях.
Обозначим:
а- сторона ромба;
М- малая диагональ;
Б- большая диагональ.
Поскольку поворот фигуры производится относительно ось перпендикулярной большой диагонали, то все линии параллельные оси поворота не изменят свой размер на проекции. В том числе и малая диагональ.
Большая же диагональ с проектируется на плоскость в размер: Б*cos(альфа) и эта величина должна быть равна малой диагонали, поскольку мы хотим получить квадрат.
М=Б*cos(альфа)
Из ромба имеем.
М=2а*sin(30)
Б=2а*cos(30)
Подставляем.
2а*sin(30)=2а*cos(30)cos(альфа)
cos(альфа)=sin(30)/cos(30)=tg(30)=1/sqr(3)
альфа=arccos(1/sqr(3))=54.7356103172 градуса ≈136839/2500
комментировать
в избранное
ссылка
отблагодарить
1
Rafail
[125K]
2 дня назад
Прежде всего условие задачи — неполное и оттого неопределённое. Представьте себе, что ромб вращается вокруг большей диагонали (в принципе на на 180°). Тот чертёж, который Вы хотели начертить, относится только к такому положению ромба, когда его малая диагональ параллельна заданной плоскости. Только тогда угол между плоскостью ромба и заданной плоскостью (или как Вы написали, между ромбом и плоскостью), который Вы обозначили alpha) будет равен углу меду большой диагональю ромба и её проекцией на плоскость ромба, и равен arccos(1/√3)=0,955 радиан или 54,7°.
Но во всех других положениях он будет больше, и в пределе будет приближаться к 90°.
Поэтому в той редакции, как Вы написали, задача имеет бесчисленное множество решений, вида
alpha = arccos(sin(фи)/√3), где угол фи — это угол, на который повёрнут ромб повёрнут ромб вокруг своей большей диагонали.
Для однозначного решения нужно указать положение ромба (например, указав угол между малой диагональю ромба и её проекцией на заданную плоскость.
в избранное
ссылка
отблагодарить
Евгений Борисович
[715]
Абсолютно неверный ответ. Ромб перейдет в квадрат лишь в одном случае.
В остальных — ромб переходит в параллелограмм.
— 2 дня назад
Георгий22
[122]
Условие вполне определённое. Сказано, что альфа — угол между плоскостями, следовательно, большая диагональ перпендикулярна прямой пересечения, а так как малая диагональ перпендикулярна большой, то малая диагональ параллельна прямой пересечения, а потому и плоскости проецирования.
— 2 дня назад
Rafail
[125K]
Евгений Борисович. Вы безусловно правы. Признаю свою ошибку.
— 2 дня назад
комментировать
1
![]()
Евгений Борисович
[715]
2 дня назад
Ответ уже дали. Повторять не буду.
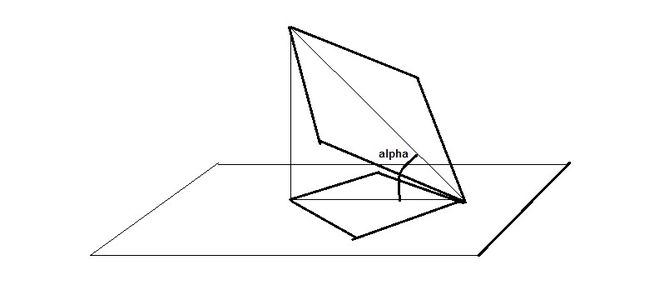
Чертеж в вопросе какой-то несуразный. Привожу более наглядный.
Проекцией ромба может быть ромб, в частности квадрат, или параллелограмм.
Более интересен такой вопрос:
При каком угле α между ромбом, со стороной 4, и плоскостью, проекцией ромба будет параллелограмм с углами 60º и 120º, и сторонами a и b?
P.S. Может задать вопрос отдельно?
в избранное
ссылка
отблагодарить
Mefody66
[28.7K]
Да, лучше задать отдельный вопрос. А почему у ромба сторона равна 4?
— 1 день назад
Евгений Борисович
[715]
Для удобства вычислений.
Я вопросе взял проекцию — параллелограмм со сторонами a и b = 2.
Всё равно, ответ не очень красивый. Подбирать нет времени.
— 1 день назад
комментировать
1
Георгий22
[122]
2 дня назад

Пояснение: малая диагональ равна своей проекции, поскольку параллельна плоскости, на которую и делается проекция. А так как у квадрата диагонали равны, то проекция большой диагонали равна малой диагонали.
P.S. Прошу прощения, что заново пишу ответ; не знаю, как восстановить старый.
комментировать
в избранное
ссылка
отблагодарить
0
![]()
дядел
[1.8K]
2 дня назад
В принципе задача не сложная. Нужно только вспомнить определения основных тригонометрических функций. А далее рассуждаем.
Малая диагональ ромба равна его стороне, а большая √3. нужно чтобы в проекции диагонали были равны. Для этого запишем cos(alpha)=1/√3. Тогда arccos(1/√3)=54.7°
Для пояснения: у ромба диагонали разновеликие, у квадрата одинаковые.
У исходного ромба сторона и малая диагональ это 1, а большая диагональ √3.
У проекции получаются диагонали 1.
комментировать
в избранное
ссылка
отблагодарить
0
![]()
Nasos
[42.1K]
2 дня назад
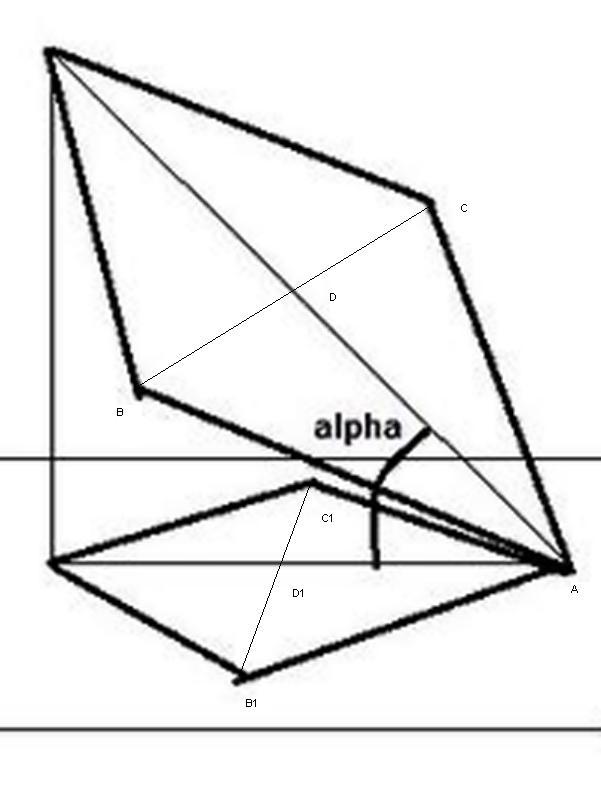
Длина отрезка AD равна (sqr(2))/2, а длина отрезка AD1 равна 1/2
Чтобы отрезок AD дал проекцию AD1, угол alpha должен быть 45 градусов, ибо
sec(45) = sqr(2).
Ответ: угол alpha равен 45 градусов.
в избранное
ссылка
отблагодарить
Георгий22
[122]
Это почему у Вас отрезок АD=√2/2?
— 2 дня назад
Nasos
[42.1K]
Потому что я ошибся, нужно было √3/2
Оттого и угол в ответе не 45, а где-то 53.5 градусов.
— 2 дня назад
комментировать
